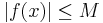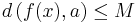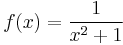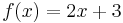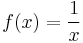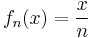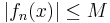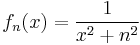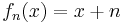Local boundedness

In mathematics, a function is locally bounded if it is bounded around every point. A family of functions is locally bounded if for any point in their domain all the functions are bounded around that point and by the same number.

Contents

Locally bounded function

A real-valued or complex-valued function f defined on some topological space X is called locally bounded if for any x0 in X there exists a neighborhood A of x0 such that f (A) is a bounded set, that is, for some number M>0 one has

|f(x)|\le M

for all x in A.

That is to say, for each x one can find a constant, depending on x, which is larger than all the values of function in the neighborhood of x. Compare this with a bounded function, for which the constant does not depend on x. Obviously, if a function is bounded then it is locally bounded. The converse is not true in general.

This definition can be extended to the case when f takes values in some metric space. Then the inequality above needs to be replaced with

d\left(f(x), a\right)\le M

for all x in A, where d is the distance function in the metric space, and a is some point in the metric space. The choice of a does not affect the definition. Choosing a different a will at most increase the constant M for which this inequality is true.

Examples

f(x)=\frac{1}{x^2%2B1}\,

is bounded, because 0≤ f (x) ≤ 1 for all x. Therefore it is also locally bounded.

f(x)=2x%2B3\,

is not bounded, as it becomes arbitrarily large. However, it is locally bounded because for each a, |f(x)| ≤ M in the neighborhood (a - 1,a + 1), where M = 2|a|+5.

f(x)=\frac{1}{x}\,

for x ≠ 0 and taking the value 0 for x=0 is not locally bounded. In any neighborhood of 0 this function takes values of arbitrarily large magnitude.

Locally bounded family

A set (also called a family) U of real-valued or complex-valued functions defined on some topological space X is called locally bounded if for any x0 in X there exists a neighborhood A of x0 and a positive number M such that

|f(x)|\le M

for all x in A and f in U. In other words, all the functions in the family must be locally bounded, and around each point they need to be bounded by the same constant.

This definition can also be extended to the case when the functions in the family U take values in some metric space, by again replacing the absolute value with the distance function.

Examples

f_n(x)=\frac{x}{n}

where n = 1, 2, ... is uniformly bounded. Indeed, if x0 is a real number, one can choose the neighborhood A to be the interval (x0-1, x0+1). Then for all x in this interval and for all n≥1 one has

|f_n(x)|\le M

with M=|x0|+1.

f_n(x)=\frac{1}{x^2%2Bn^2}

is locally bounded. For any x0 one can choose the neighborhood A to be R itself. Then we have

|f_n(x)|\le M

with M=1. Note that the value of M does not depend on the choice of x0 or its neighborhood A. This family is then not only locally bounded, it is also uniformly bounded.

f_n(x)=x%2Bn

is not locally bounded. Indeed, for any x0 the values fn(x0) cannot be bounded as n tends toward infinity.

Topological vector spaces

Local boundedness may also refer to a property of topological vector spaces, or of functions from a topological space into a topological vector space.

Locally bounded topological vector spaces

Let X be a topological vector space. Then a subset B ⊂ X is bounded if for each open neighborhood U of 0 in X there exists a number m > 0 such that

B ⊂ xU for all x > m.

A topological vector space is said to be locally bounded if X admits a bounded open neighborhood of 0.

Locally bounded functions

Let X be a topological space, Y a topological vector space, and f : X → Y a function. Then f is locally bounded if each point of X has a neighborhood whose image under f is bounded.

The following theorem relates local boundedness of functions with the local boundedness of topological vector spaces:

Theorem. A topological vector space X is locally bounded if and only if the identity mapping 1 : X → X is locally bounded.

External links